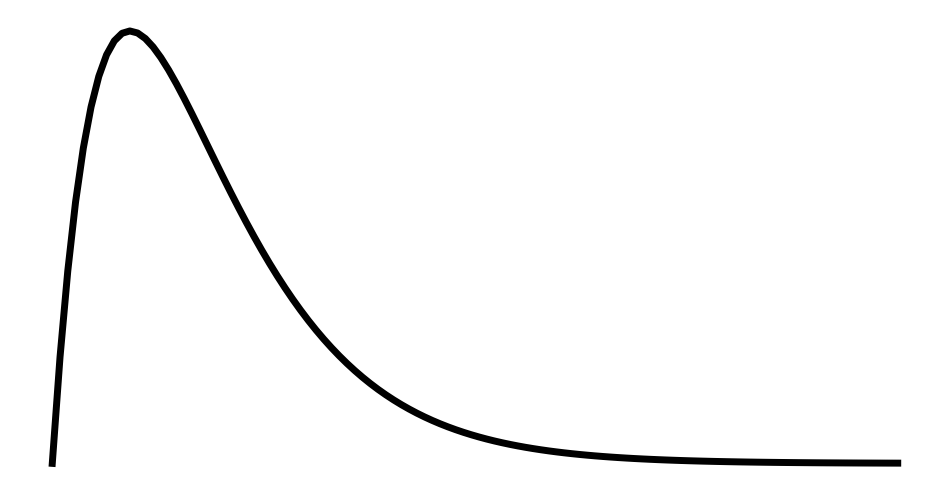
アーラン分布は代表的な確率分布の1つであるガンマ分布のうちの一つです。
また、アーラン分布は指数分布からも導出することも出来ます。
アーラン分布は体重の分布やウイルスの潜伏期間などに利用されています。
| 確率密度関数 | \( \begin{eqnarray*} f(x) = \begin{cases} \frac{\lambda^n }{(n-1)!} x^{n-1} e^{-\lambda x} & (x \geq 0)\\ 0 & (x<0) \end{cases} \end{eqnarray*} \) |
| 定数 | \( n \in \mathbb{N}, \quad \lambda > 0\) |
| 平均値 | \( \displaystyle \frac{n}{\lambda} \) |
| 分散 | \( \displaystyle \frac{n}{\lambda^2} \) |
定義
自然数\( n \in \mathbb{N} \)と正の実数\( \lambda >0 \)を用いて、
$$ \begin{eqnarray*} f(x) = \begin{cases} \frac{\lambda^n}{(n-1)!} x^{n-1} e^{-\lambda x} & (x \geq 0)\\ 0 & (x<0) \end{cases} \end{eqnarray*} $$と定義される確率分布をアーラン分布といい、\( Er(n, \lambda) \)と書く。
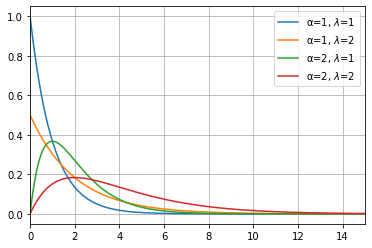
アーラン分布は、ガンマ分布\( Ga(\alpha, \lambda) \)の1つで、\( \alpha \)が自然数のとき、すなわち、\( \alpha=n \)を代入したものです。
\( n \)個の確率変数\( X_1, \cdots, X_n \)がそれぞれ独立で指数分布\( Ex(\lambda) \)に従うとする。
このとき、\( X_1 + \cdots + X_n \)はアーラン分布に従う。
\( X_1 + \cdots + X_n \)の確率密度関数\( f_n \)が
$$ \begin{eqnarray*} f_n(x) = \begin{cases} \frac{\lambda^n}{(n-1)!} x^{n-1} e^{-\lambda x} & (x \geq 0)\\ 0 & (x<0) \end{cases} \end{eqnarray*} $$を示せばよい。これを\( n \)に関する帰納法で示す.
\( n=1 \)のとき、確率変数\( X_1 \)は指数分布に従い、\( X_1 \)の確率密度関数は、
$$ f_1 (x) = \left\{ \begin{array}{ll} \lambda e^{-\lambda x} & (x \geq 0)\\ 0 & (x<0) \end{array} \right. $$であり、確かにアーラン分布に従う。
次に、\( k \geq 1 \)のとき、\( Z = X_1 + \cdots + X_k \)の確率密度関数は\( f_k \)であると仮定する。
\( Z + X_{k+1} \)の確率密度関数\( f_{k+1} \)を計算する。
それぞれの確率変数は独立で、\( X_{k+1} \)は指数分布に従うことから、
$$ \begin{eqnarray*} f_{k+1}(x) &=& \int_{-\infty}^{+\infty} f_1 (y) f_k (x-y) dy \\ &=& \int_0^{x} \lambda e^{-\lambda y} \cdot \frac{\lambda^k}{(k-1)!} (x-y)^{k-1} e^{-\lambda (x-y)} dy \\ &=& \frac{\lambda^{k+1}}{(k-1)!} e^{-\lambda x} \int_0^x (x-y)^{k-1} dy \\ &=& \frac{\lambda^{k+1}}{(k-1)!} e^{-\lambda x} \left[ -\frac{(x-y)^k}{k} \right]_0^x \\ &=& \frac{\lambda^{k+1}}{(k-1)!} e^{-\lambda x} \cdot \frac{x^k}{k} \\ &=& \frac{\lambda^{k+1}}{k!} x^k e^{-\lambda x} \end{eqnarray*} $$これは\( X_1 + \cdots X_{k+1} \)がアーラン分布\( Er(k+1,\lambda) \)に従うことを示している。