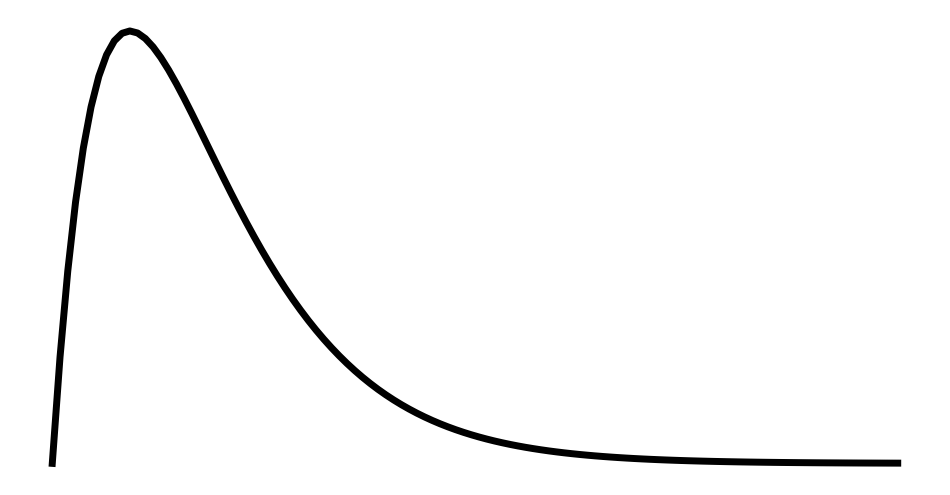
ガンマ分布とは指数分布の一般化であり、統計学において様々な場合で現れます。
具体的には、体重の分布やウイルスの潜伏期間などがガンマ分布に従うと言われています。
| 確率密度関数 | \begin{eqnarray*} f(x) = \begin{cases} \frac{\lambda^\alpha}{\Gamma(\alpha)} x^{\alpha-1} e^{-\lambda x} & (x \geq 0)\\ 0 & (x<0) \end{cases} \end{eqnarray*} |
| 定数 | \( \displaystyle \alpha>0, \quad \lambda>0, \quad \Gamma(\alpha) = \int_0^\infty x^{\alpha-1} e^{-x} dx \) |
| 平均値 | \( \displaystyle \frac{\alpha}{\lambda} \) |
| 分散 | \( \displaystyle \frac{\alpha}{\lambda^2} \) |
定義
定数\( \alpha>0, \, \lambda>0 \)を用いて、確率密度関数
$$ \begin{eqnarray*} f(x) = \begin{cases} \frac{\lambda^\alpha}{\Gamma(\alpha)} x^{\alpha-1} e^{-\lambda x} & (x \geq 0)\\ 0 & (x<0) \end{cases} \end{eqnarray*} $$で定義される確率分布をガンマ分布といい、\( Ga(\alpha, \lambda) \)と書く。ここで、
$$ \Gamma(\alpha) = \int_0^\infty x^{\alpha-1} e^{-x} dx $$である。
\( \Gamma(\alpha) \)をガンマ関数といい、\( f(x) \)が積分して\( 1 \)になるように定められています。
したがって、ガンマ分布\( Ga(\alpha, \lambda) \)は確率密度関数であることが分かります。
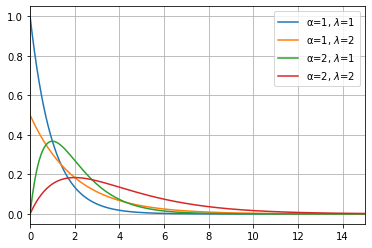
また、\( \Gamma(1)=1 \)であるから、ガンマ分布\( Ga(1, \lambda) \)は指数分布となります。
平均値
ガンマ分布\( Ga(\alpha, \lambda) \)の平均値は\( \displaystyle \frac{\alpha}{\lambda} \)である。
確率変数\( X \)が指数分布\( Ga(\alpha, \lambda) \)に従うとする。
このとき、平均値\( E[X] \)を計算する。ガンマ関数の定義式から、
$$\begin{eqnarray*} E[X] &=& \int_{-\infty}^\infty xf(x)dx \\ &=& \int_0^\infty \frac{\lambda^\alpha}{\Gamma(\alpha)} x^\alpha e^{-\lambda x} dx \\ &=& \left[ -\frac{\lambda^{\alpha-1}}{\Gamma(\alpha)} x^\alpha e^{-\lambda x} \right]_0^\infty + \int_0^\infty \frac{\lambda^{\alpha-1}}{\Gamma(\alpha)} \alpha x^{\alpha-1} e^{-\lambda x} dx \\ &=& 0 + \frac{\alpha}{\lambda \Gamma(\alpha)} \int_0^\infty x^{\alpha-1} e^{-x} dx \\ &=& \frac{\alpha}{\lambda} \end{eqnarray*}$$
分散
ガンマ分布\( Ga(\alpha, \lambda) \)の分散は\( \displaystyle \frac{\alpha}{\lambda^2} \)である。
確率変数\( X \)が指数分布\( Ga(\alpha, \lambda) \)に従うとする。
まず、\( E[X^2] \)を計算する。
$$ \begin{eqnarray*} E[X^2] &=& \int_{-\infty}^\infty x^2 f(x)dx \\ &=& \int_0^\infty \frac{\lambda^\alpha}{\Gamma(\alpha)} x^{\alpha+1} e^{-\lambda x} dx \\ &=& \left[ -\frac{\lambda^{\alpha-1}}{\Gamma(\alpha)} x^{\alpha+1} e^{-\lambda x} \right]_0^\infty + \int_0^\infty \frac{\lambda^{\alpha-1}}{\Gamma(\alpha)} (\alpha+1) x^\alpha e^{-\lambda x} dx \\ &=& 0 + \frac{(\alpha+1)E[X]}{\lambda} = \frac{\alpha(\alpha+1)}{\lambda^2} \end{eqnarray*} $$したがって、分散\( V[X] \)は
$$ V[X] = E[X^2] -E[X]^2 = \frac{\alpha(\alpha+1)}{\lambda^2} – \frac{\alpha^2}{\lambda^2} = \frac{\alpha}{\lambda^2} $$
再生性
\(X, Y\)をそれぞれガウス分布\( Ga(\alpha_1, \lambda), \, Ga(\alpha_2, \lambda) \)に従う互いに独立な確率変数とする。
このとき、\( X+Y \)は、ガウス分布\( Ga(\alpha_1 + \alpha_2, \lambda) \)に従う。
ガウス分布の再生性を証明するために、まず、次のガウス関数とベータ関数の関係式を求める。
\( \alpha>0, \, \beta > 0 \)に対して、
$$ B(\alpha,\beta) = \frac{\Gamma(\alpha) \Gamma(\beta)}{\Gamma(\alpha+\beta)} $$が成り立つ。ただし、\( \displaystyle B(\alpha,\beta) = \int_0^1 x^{\alpha-1} (1-x)^{\beta-1} dx \)であり、
\( B(\alpha, \beta) \)をベータ関数という。
$$ \begin{eqnarray*} \Gamma(\alpha) \Gamma(\beta) &=& \int_0^\infty x^{\alpha-1} e^{-x} dx \int_0^\infty y^{\beta-1} e^{-y} dy \\ &=& \int_0^\infty \int_0^\infty x^{\alpha-1} y^{\beta-1} e^{-x-y} dxdy \end{eqnarray*} $$ここで、\( x=uv, \, y=u(1-v) \)で置換積分する。
$$ \{ (x,y) \, | \, x,y \in (0,\infty) \} = \{ (u,v) \, | \, u \in (0,\infty), v \in (0,1) \} $$ $$ \begin{eqnarray*} dxdy &=& \left| \mathrm{det} \begin{pmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \\ \end{pmatrix} \right| dudv \\ &=& \left| \mathrm{det} \begin{pmatrix} v & u \\ (1-v) & -u \\ \end{pmatrix} \right| dudv \\ &=& u \, dudv \end{eqnarray*} $$以上より、
$$ \begin{eqnarray*} \Gamma(\alpha) \Gamma(\beta) &=& \int_0^\infty \int_0^\infty (uv)^{\alpha-1} (u(1-v))^{\beta-1} e^{-u} u \, dvdu \\ &=& \int_0^\infty u^{\alpha+\beta-1} e^{-u} du \int_0^1 v^{\alpha-1} (1-v)^{\beta-1} dv \\ &=& \Gamma(\alpha+\beta) B(\alpha,\beta) \end{eqnarray*} $$したがって、補題が成り立つ。
補題の証明のために定義したベータ関数は、ベータ分布の定義に使用されています。
\( X, Y, X+Y \)の確率密度関数をそれぞれ\( f_X, f_Y, f_{X+Y} \)とおく。
それぞれ独立であるから、
$$ \begin{eqnarray*} f_{X+Y}(x) &=& \int_0^x f_X(y) f_Y(x-y) dy \\ &=& \int_0^x \left\{ \frac{\lambda^{\alpha_1}}{\Gamma(\alpha_1)} y^{\alpha_1-1} e^{-\lambda y} \right\} \left\{ \frac{\lambda^{\alpha_2}}{\Gamma(\alpha_2)} (x-y)^{\alpha_2-1} e^{-\lambda (x-y)} \right\} dy \\ &=& \frac{\lambda^{\alpha_1+\alpha_2}}{\Gamma(\alpha_1)\Gamma(\alpha_2)} e^{-\lambda x} \int_0^x y^{\alpha_1-1} (x-y)^{\alpha_2-1} dy \end{eqnarray*} $$ここで、\( y=xz \)とおくと、\( dy = x \, dz \)で、\( z \)の積分区間は\( [0,1) \)であることと、
補題で示したガンマ関数とベータ関数の関係式から、
$$ \begin{eqnarray*} f_{X+Y}(x) &=& \frac{\lambda^{\alpha_1+\alpha_2}}{\Gamma(\alpha_1)\Gamma(\alpha_2)} x^{\alpha_1+\alpha_2-1} e^{-\lambda x} \int_0^1 z^{\alpha_1-1} (1-z)^{\alpha_2-1} dz \\ &=& \frac{\lambda^{\alpha_1+\alpha_2}}{\Gamma(\alpha_1)\Gamma(\alpha_2)} x^{\alpha_1+\alpha_2-1} e^{-\lambda x} B(\alpha_1,\alpha_2) \\ &=& \frac{\lambda^{\alpha_1+\alpha_2}}{\Gamma(\alpha_1+\alpha_2)} x^{\alpha_1+\alpha_2-1} e^{-\lambda x} \end{eqnarray*} $$したがって、\( X+Y \)は\( Ga(\alpha_1+\alpha_2, \lambda) \)に従う。