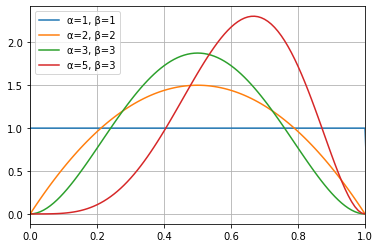
ベータ関数は変数を変更することによって様々な形に変えることが出来る分布です。
ベータ分布となる現象は少ないですが、確率分布の形が分かっているときにその形にあてはめたいときにベータ分布が使用されます。
| 確率密度関数 | \begin{eqnarray*} f(x) = \begin{cases} \displaystyle \frac{x^{\alpha-1} (1-x)^{\beta-1}}{B(\alpha, \beta)} & (0<x<1) \\ 0 & (\mbox{その他}) \end{cases} \end{eqnarray*} |
| 定数 | \( \displaystyle \alpha>0, \quad \beta>0, \quad B(\alpha, \beta) = \int_0^1 x^{\alpha-1} (1-x)^{\beta-1} dx \) |
| 平均値 | \( \displaystyle \frac{\alpha}{\alpha+\beta} \) |
| 分散 | \( \displaystyle \frac{\alpha\beta}{(\alpha+\beta)^2 (\alpha+\beta+1)} \) |
定義
定数\( \alpha>0, \, \beta>0 \)を用いて、確率密度関数
$$ \begin{eqnarray*} f(x) = \begin{cases} \displaystyle \frac{x^{\alpha-1} (1-x)^{\beta-1}}{B(\alpha, \beta)} & (0<x<1) \\ 0 & (\mbox{その他}) \end{cases} \end{eqnarray*} $$で定義される確率分布をベータ分布といい、\( Be(\alpha,\beta) \)と書く。ここで、
$$ B(\alpha,\beta) = \int_0^1 x^{\alpha-1} (1-x)^{\beta-1} dx $$である。
\( B(\alpha,\beta) \)をベータ関数といい、\( f(x) \)が積分して\(1\)になるように定められています。
したがって、ベータ分布\( Be(\alpha,\beta) \)は確率密度関数であることが分かります。
平均値
ベータ分布\( Be(\alpha,\beta) \)の平均値は\( \displaystyle \frac{\alpha}{\alpha+\beta} \)である。
確率変数\( X \)がベータ関数\( Be(\alpha,\beta) \)に従うとする。
平均値\( E[X] \)を計算する。
$$ \begin{eqnarray*} E[X] &=& \int_{-\infty}^{+\infty} xf(x) dx \\ &=& \frac{1}{B(\alpha,\beta)} \int_0^{1} x^{\alpha} (1-x)^{\beta-1} dx \\ &=& \frac{B(\alpha+1,\beta)}{B(\alpha,\beta)} \end{eqnarray*} $$ここで、\( B(\alpha+1,\beta) \)を計算する。
$$ \begin{eqnarray*} B(\alpha+1,\beta) &=& \int_0^1 x^\alpha (1-x)^{\beta-1} dx \\ &=& \left[ -\frac{1}{\beta} x^\alpha (1-x)^\beta \right]_0^1 + \int_0^1 \frac{\alpha}{\beta} x^{\alpha-1} (1-x)^\beta dx \\ &=& \frac{\alpha}{\beta} \int_0^1 x^{\alpha-1} (1-x)^{\beta-1} (1-x) dx \\ &=& \frac{\alpha}{\beta} \left\{ \int_0^1 x^{\alpha-1} (1-x)^{\beta-1} dx \; – \int_0^1 x^\alpha (1-x)^{\beta-1} dx \right\} \\ &=& \frac{\alpha}{\beta} \{ B(\alpha,\beta) \, – B(\alpha+1,\beta) \} \end{eqnarray*} $$上式を解くと、
$$ B(\alpha+1,\beta) = \frac{\alpha}{\alpha+\beta} B(\alpha,\beta) $$したがって、\( \displaystyle E[X] = \frac{\alpha}{\alpha+\beta} \)が成り立つ。
分散
ベータ分布\( Be(\alpha,\beta) \)の分散は\( \displaystyle \frac{\alpha \beta}{(\alpha+\beta)^2 (\alpha+\beta+1)} \)である。
確率変数\( X \)がベータ分布\( B(\alpha,\beta) \)に従うとする。
まず、\( E[X^2] \)を計算する。
$$ \begin{eqnarray*} E[X^2] &=& \int_{-\infty}^{+\infty} x^2 f(x) dx \\ &=& \frac{1}{B(\alpha,\beta)} \int_0^1 x^{\alpha+1} (1-x)^{\beta-1} dx \\ &=& \frac{B(\alpha+2,\beta)}{B(\alpha,\beta)} \end{eqnarray*} $$平均値の証明の過程より、\( \displaystyle B(\alpha+1,\beta) = \frac{\alpha}{\alpha+\beta} B(\alpha,\beta) \)であるから、
$$ \begin{eqnarray*} B(\alpha+2,\beta) &=& \frac{\alpha+1}{\alpha+\beta+1} B(\alpha+1,\beta) \\ &=& \frac{\alpha(\alpha+1)}{(\alpha+\beta) (\alpha+\beta+1)} B(\alpha,\beta) \end{eqnarray*} $$ゆえに$$ E[X^2] = \frac{\alpha(\alpha+1)}{(\alpha+\beta) (\alpha+\beta+1)} $$である。したがって、\( V[X] \)は
$$ \begin{eqnarray*} V[X] &=& E[X^2] \, – E[X]^2 \\
&=& \frac{\alpha(\alpha+1)}{(\alpha+\beta) (\alpha+\beta+1)} \, – \frac{\alpha^2}{(\alpha+\beta)^2} \\
&=& \frac{\alpha \beta}{(\alpha+\beta)^2 (\alpha+\beta+1)} \end{eqnarray*} $$