【統計学】幾何分布とは定義と性質まとめ【証明】

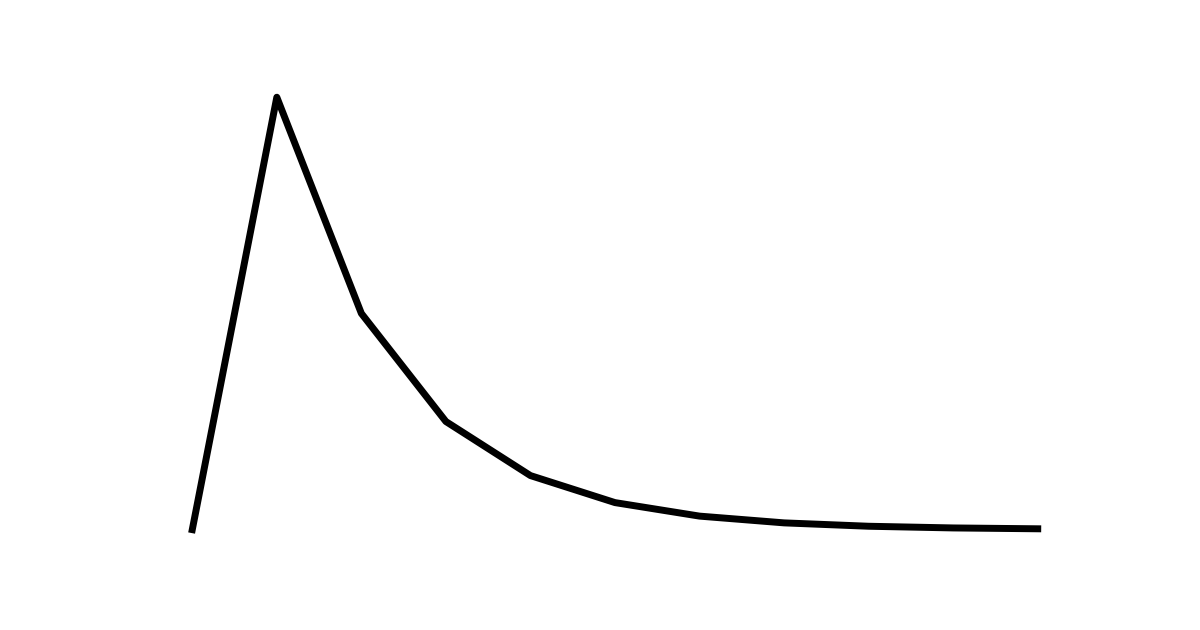
二項分布とは、成功か失敗かの2択の試行を繰り返した際、$ k $回目に初めて成功するか、その確率を求めるものです。
幾何分布は、災害が発生する確率を求める際などに使用されます。

定数	$ p \quad (0<p<1) $
確率質量関数	$ f(k) = p(1-p)^{k-1} $
平均値	$ \displaystyle \frac{1}{p} $
分散	$ \displaystyle \frac{1-p}{p^2} $

定義
- 幾何分布の確率質量関数
平均値
分散
無記憶性

定義

二項分布でも定義した、ベルヌーイ試行から定義します。
コインの裏表や成功・失敗のような$0$か$1$で表せる思考をベルヌーイ試行といいます。
ここで、ベルヌーイ試行を行った際、$ k $ 回目に初めて成功する確率を幾何分布といいます。

ベルヌーイ試行の定義

確率変数$ Z = 0, 1 $に対して、
$$ P(Z=1)=p, \quad P(Z=0)=1-p \qquad (0 \leq p \leq 1) $$を満たす試行のことを成功確率$ p $のベルヌーイ試行という。

幾何分布の確率質量関数

成功確率$ p $のベルヌーイ試行を繰り返し行い、$ k $回目に初めて成功する確率を幾何分布といい、$ Geo(p) $と書く。
$ Geo(p) $の確率質量関数は以下となる。
$$ f(k) = p(1-p)^{k-1} $$

幾何分布が確率分布であることの証明

$ 0<p<1 $であるから、無限等比級数の和は収束するので、
$$ \sum_{i=0}^\infty f(i) = \sum_{i=0}^\infty p(1-p)^{i-1} = 1 $$

平均値

幾何分布$ Geo(p) $の平均値は$ \displaystyle \frac{1}{p} $である。

証明

確率変数$ X $が$ Geo(p) $に従うとする。平均値$ E[X] $を計算する。
ここで、確率分布であることから、
$$ \begin{eqnarray*} 1 &=& \sum_{i=0}^\infty f(i) \\ &=& \sum_{i=0}^\infty \{if(i) – (i-1)f(i) \} \\ &=& \sum_{i=0}^\infty \{ ip(1-p)^{i-1} – (i-1)p(1-p)^{i-1} \} \\ &=& \sum_{i=0}^\infty ip(1-p)^{i-1} – (1-p) \sum_{i=0}^\infty ip(1-p)^{i-1} \\ &=& p \sum_{i=0}^\infty ip(1-p)^{i-1} \\ &=& pE[X] \end{eqnarray*} $$したがって、$ \displaystyle E[X] = \frac{1}{p} $である。

分散

幾何分布$ Geo(p) $の分散は$ \displaystyle \frac{1-p}{p^2} $である。

証明

確率変数$ X $が$ Geo(p) $に従うとする。まずは$ E[X^2] $から計算する。
平均値は$ \displaystyle \frac{1}{p} $であることから、
$$ \begin{eqnarray*} \frac{2}{p} &=& \sum_{i=0}^\infty 2if(i) \\ &=& \sum_{i=0}^\infty \{ i^2 – (i-1)^2 + 1 \} f(i) \\ &=& \sum_{i=0}^\infty \{ i^2 – (i-1)^2 + 1 \} p(1-p)^{i-1} \\ &=& \sum_{i=0}^\infty i^2 p(1-p)^{i-1} \, – (1-p) \sum_{i=0}^\infty i^2 p(1-p)^{i-1} + \sum_{i=0}^\infty p(1-p)^{i-1} \\ &=& p \sum_{i=0}^\infty i^2 p(1-p)^{i-1} + \sum_{i=0}^\infty p(1-p)^{i-1} \\ &=& pE[X^2] + 1 \end{eqnarray*} $$したがって、
$$ E[X^2] = \frac{2-p}{p^2} $$以上より、分散$ V[X] $は
$$ V[X] = E[X^2] – E[X]^2 = \frac{2-p}{p^2} – \frac{1}{p^2} = \frac{1-p}{p^2} $$

無記憶性

無記憶性とは、前までの事象に依存しないという性質です。
例えば、「災害が発生したから次は発生しないということはない」ということです。
離散型の確率分布で無記憶性を持つものは指数分布のみとなります。

確率変数$ X $が幾何分布$ Geo(p) $に従うとする。このとき、
$$ P(X > m+n \, | \, X > m)=P(X > n) \qquad (m > 0, n > 0) $$が成り立つ。これを無記憶性を持つという。
逆に、離散分布において、無記憶性を持つ分布は指数分布のみである。

幾何分布が無記憶性を持つことの証明

整数$ m \geq 0 $に対して、
$$ \begin{eqnarray*} P(X > m) &=& \sum_{i=m+1}^\infty p(1-p)^{i-1} \\ &=& p(1-p)^m \sum_{i=1}^\infty (1-p)^{i-1} \\ &=& (1-p)^m \end{eqnarray*} $$条件付確率の定義より、
$$ P( X > m+n \, | \, X > m ) = \frac{P( X > m+n, \, X > m )}{P(X > m )} $$さらに、事象について、$ \{ X > m+n \, | \, X > m \} = \{ X > m+n \} $が成り立つので、
$$ \begin{eqnarray*} P( X > m+n \, | \, X > m ) &=& \frac{P( X > m+n )}{P(X > m )} \\ &=& \frac{(1-p)^{m+n}}{(1-p)^m} \\ &=& (1-p)^n \\ &=& P(X > n) \end{eqnarray*} $$したがって、無記憶性が成り立つ。

無記憶性を持つ離散分布は幾何分布のみであることの証明

確率変数$ X $が無記憶性を持つ離散分布に従うと仮定する。
$$ P(X > m+n \, | \, X > m)=P(X > n) \qquad (m > 0, n > 0) $$ここで、条件付確率の定義と事象について、$ \{ X > m+n \, | \, X > m \} = \{ X > m+n \} $が成り立つので、
$$ P(X>m+n) = P(X>m) P(X>n) $$したがって、
$$ \begin{eqnarray*} P(X>m) &=& P(X>m-1)P(X>1) \\ &=& P(X>m-2)P(X>1)^2 \\ && \cdots \\ &=& P(X>1)^m \end{eqnarray*} $$ここで、$ P(X>0) = 1 $であるから、
$ 0 $以上の整数$ m \geq 0 $に対して、$ P(X>m) = P(X>1)^m $が成り立つ。
$ P(X>1) = q $とおくと、
$$ \begin{eqnarray*} P(X=k) &=& P(X>k-1) \, – P(X>k) \\ &=& q^{k-1} \, – \, q^k = q^{k-1}(1-q) \end{eqnarray*} $$$ p = 1-q $とおくと、$ P(X=k) = p(1-p)^{k-1} $が成り立つ。
したがって、無記憶性を持つ離散分布は幾何分布のみである。