正規分布とは代表的な確率分布です。
自然界や人間社会の中の減少に対して当てはまります。
統計学の理論上も応用上も非常に重要です。
| 確率密度関数 | \( f(x) = \displaystyle \frac{1}{\sqrt{2\pi}\sigma} \mathrm{exp}\left\{ -\frac{(x-\mu)^2}{2 \sigma^2} \right\} \) |
| 平均値 | \( \mu \) |
| 分散 | \( \sigma^2 \) |
正規分布の定義
平均値\( \mu \)、分散\( \sigma^2 \)の正規分布の確率密度関数\( f(x) \)は、
$$ f(x) = \frac{1}{\sqrt{2\pi}\sigma}\mathrm{exp}\left\{ -\frac{(x-\mu)^2}{2 \sigma^2} \right\} $$
と定める。
平均値\( \mu \)、分散\( \sigma^2 \)の正規分布を\( N(\mu, \sigma^2) \)と表します。
特に、平均値\( 0 \)、分散\( 1 \)の正規分布 \( N(0, 1) \)を標準正規分布といいます。
正規分布(normal distribution)はガウス分布(Gaussian distribution)と呼ばれることもあります。
これは数学者C.F.ガウスに由来します。
ガウスは天文学の観測データを分析において、その測定誤差についての法則性を仮定し、そこからガウス分布が生まれました。
ここで、「正規」というのは、「ありふれた」「通常の」という意味であり、統計学において、基本となる重要な確率分布です。
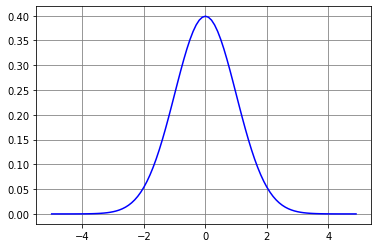
全ての\( x \in \mathbb{R} \)に対して、\( f(x) > 0\)であることは明らかなので、積分値が\( 1 \)になることを示せばよい。
$$ \begin{eqnarray*} \int_{-\infty}^{+\infty} f(x)dx &=& \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{+\infty} \mathrm{exp}\left\{ -\frac{(x-\mu)^2}{2 \sigma^2} \right\} dx \\ & = & \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{+\infty} \mathrm{exp}\left\{ -\frac{x^2}{2 \sigma^2} \right\} dx \\ & = & \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{+\infty} e^{-x^2} \sqrt2 \sigma dx \\ & = & \frac{1}{\sqrt\pi} \int_{-\infty}^{+\infty} e^{-x^2} dx \end{eqnarray*} $$ ここで、\( \displaystyle I = \int_{-\infty}^{+\infty} e^{-x^2} dx \)とおく。
$$ \begin{eqnarray*} I^2 &=& \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} e^{-(x^2 + y^2)} dxdy \\ &=& \int_{0}^{2\pi} \int_{0}^{+\infty} e^{-r^2} rdrd\theta \\ &=& 2\pi \left[ -\frac{1}{2} e^{-r^2} \right]_{0}^{+\infty} = \pi \end{eqnarray*} $$ 従って、 \( \displaystyle \int_{-\infty}^{+\infty} e^{-x^2} dx = \sqrt{\pi} \)が成り立つ。この積分をガウス積分と呼ぶ。
以上より、\( \displaystyle \int_{-\infty}^{+\infty} f(x)dx = 1 \)が成り立つ。
平均値
正規分布\( N(\mu, \sigma) \)の平均値は、\( \mu \)である。
正規分布の確率密度関数を\( f(x) \)、正規分布の確率変数を\( X \)とする。
変数変換と奇関数の積分がが\( 0 \)になることより、平均値\( E[X] \)は
$$ \begin{eqnarray*} E[X] &=& \int_{-\infty}^{+\infty} x f(x)dx \\ &=& \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{+\infty} x \mathrm{exp}\left\{ -\frac{(x-\mu)^2}{2 \sigma^2} \right\} dx \\ &=& \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^{+\infty} (x+\mu) \mathrm{exp}\left\{ -\frac{x^2}{2 \sigma^2} \right\} dx \\ &=& \frac{\mu}{\sqrt{2\pi}\sigma} \int_{-\infty}^{+\infty} \mathrm{exp}\left\{ -\frac{x^2}{2 \sigma^2} \right\} dx \\ &=& \frac{\mu}{\sqrt{\pi}} \int_{-\infty}^{+\infty} e^{-x^2} dx = \mu \\ \end{eqnarray*} $$ ここで、最後の等式は、ガウス積分より成り立つ。
分散
正規分布\( N(\mu, \sigma) \)の分散は、\( \sigma^2 \)である。
正規分布の確率密度関数を\( f(x) \)、正規分布の確率変数を\( X \)とする。
正規分布の平均が\( \mu \)となることから、正規分布の分散\( V[X] \)は
$$ \begin{eqnarray*} V[X] &=& \int_{-\infty}^{+\infty} (x-\mu)^2 f(x)dx \\
&=& \int_{-\infty}^{+\infty} \frac{(x-\mu)^2}{\sqrt{2\pi}\sigma} \mathrm{exp}\left\{ -\frac{(x-\mu)^2}{2 \sigma^2} \right\} dx \\
&=& \frac{2\sigma^2}{\sqrt{\pi}} \int_{-\infty}^{+\infty} x^2 e^{-x^2} dx \\
&=& \frac{\sigma^2}{\sqrt{\pi}} \int_{-\infty}^{+\infty} x \left( -e^{-x^2} \right)^\prime dx \\
&=& \frac{\sigma^2}{\sqrt{\pi}} \left\{ \left[ -xe^{-x^2} \right]_{-\infty}^{+\infty} + \int_{-\infty}^{+\infty} e^{-x^2} dx \right\} \\
&=& \sigma^2 \end{eqnarray*}$$
再生性
\( X, Y \)をそれぞれ正規分布\( N(\mu_1, \sigma_1^2), N( \mu_2, \sigma_2^2 ) \)に従う互いに独立な確率変数とする。
このとき\( X+Y \)は、\( N(\mu_1+\mu_2, \sigma_1^2+\sigma_2^2) \)に従う。
\(X, Y, X+Y \)の確率密度関数をそれぞれ\( f_X, f_Y, f_{X+Y} \)とおく。
\( X \)と\( Y \)が独立であることから、
$$ \begin{eqnarray*} f_{X+Y}(x) &=& \int_{-\infty}^{+\infty} f_X(x-y) f_Y(y) dy \\ &=& \frac{1}{2\pi\sigma_1\sigma_2} \int_{-\infty}^{+\infty}\mathrm{exp} \left\{ -\frac{((x-y)-\mu_1)^2}{\sigma_1^2} – \frac{(y-\mu_2)^2}{\sigma_2^2} \right\} dy \end{eqnarray*} $$ 最終項の指数について、
$$ -\frac{((x-y)-\mu_1)^2}{\sigma_1^2} – \frac{(y-\mu_2)^2}{\sigma_2^2} = \: – \frac{\sigma_1^2 + \sigma_2^2}{2\sigma_1^2 \sigma_2^2} (y – C)^2 – \frac{(x-(\mu_1+\mu_2))^2}{2(\sigma_1^2+\sigma_2^2)} $$ ただし、\( \displaystyle C = \frac{x\sigma_2^2 + \mu_1\sigma_2^2 – \mu_2\sigma_1^2}{\sigma_1^2 + \sigma_2^2} \)である。ここで、ガウス積分より、
$$ \int_{-\infty}^{+\infty} \mathrm{exp} \left\{ \frac{\sigma_1^2 + \sigma_2^2}{2\sigma_1^2 \sigma_2^2} (y – C)^2 \right\} dy = \sqrt{\frac{2\pi\sigma_1^2\sigma_2^2}{\sigma_1^2 + \sigma_2^2}} $$ 以上より、
$$ \begin{eqnarray*} f_{X+Y}(x) &=& \frac{1}{2\pi\sigma_1\sigma_2} \sqrt{\frac{2\pi\sigma_1^2\sigma_2^2}{\sigma_1^2 + \sigma_2^2}} \mathrm{exp} \left\{-\frac{(x-(\mu_1+\mu_2))^2}{2(\sigma_1^2+\sigma_2^2)} \right\} \\ &=& \frac{1}{\sqrt{2\pi(\sigma_1^2 + \sigma_2^2)}} \mathrm{exp} \left\{-\frac{(x-(\mu_1+\mu_2))^2}{2(\sigma_1^2+\sigma_2^2)} \right\} \end{eqnarray*} $$ \( f_{X+Y} \)は、正規分布\( N(\mu_1+\mu_2, \sigma_1^2+\sigma_2^2) \)の確率密度関数である。