負の二項分布は成功成功か失敗かの2択の試行を繰り返し、\( n \)回目の成功までに、\( k \)回失敗する確率を求めたものです。
幾何分布の一般化したものであり、具体的には災害や事故の発生回数を求める際に利用されます。
| 定数 | \( n, p \quad (0<p<1) \) |
| 確率質量関数 | \( f(k | n, p) = \begin{pmatrix}k+n-1\\k\end{pmatrix} p^n (1-p)^k \) |
| 平均値 | \( \displaystyle \frac{n(1-p)}{p} \) |
| 分散 | \( \displaystyle \frac{n(1-p)}{p^2} \) |
定義
二項分布でも定義した、ベルヌーイ試行から定義します。
コインの裏表や成功・失敗のような\(0\)か\(1\)で表せる思考をベルヌーイ試行といいます。
ここで、ベルヌーイ試行を行った際、\( n \)回目の成功までに、\( k \)回失敗する確率を負の二項分布またはパスカル分布といいます。
確率変数\( Z = 0, 1 \)に対して、
$$ P(Z=1)=p, \quad P(Z=0)=1-p \qquad (0 \leq p \leq 1) $$を満たす試行のことを成功確率\( p \)のベルヌーイ試行という。
負の二項分布の確率質量関数
成功確率\( p \)のベルヌーイ試行を繰り返し行い、\( n \)回目の成功までに、\( k \)回失敗する確率を負の二項分布といい、\( NB(n,p) \)と書く。
\( NB(k,p) \)の確率質量関数は以下となる。
$$ f(k | n, p) = \begin{pmatrix}k+n-1\\k\end{pmatrix} p^n (1-p)^k $$
負の二項分布は幾何分布の一般化であり、\( n=1 \)を代入することで得られる。
\( i, j \)が\(i \geq j \geq 0 \)を満たす自然数のとき、二項係数\( \displaystyle \begin{pmatrix}i\\j\end{pmatrix} \)は、\( i \)個の中から\( j \)個を選ぶ組み合わせの数であり、
$$ \begin{pmatrix}i\\j\end{pmatrix} = \frac{i!}{j!(i-j)!} = \frac{\overbrace{i(i-1) \cdots (i-j+1)}^{j個}}{j(j-1) \cdots 1} $$と定義されているが、
$$ \begin{pmatrix}i\\j\end{pmatrix} = \left\{ \begin{array}{ll} \displaystyle \left. \frac{1}{j!} \left( \frac{d}{dx} \right)^j x^i \right|_{x=1} & (k \geq 0)\\ 0 & (k<0) \end{array} \right. $$と定義すると\( i, j \)がすべての整数の場合に拡張できる。
\( i<0 \)のとき、計算すると、
$$ \begin{pmatrix}i\\j\end{pmatrix} = (-1)^j \begin{pmatrix}j-i-1\\j\end{pmatrix} $$が成り立つ。
ここで、\( (x+1)^i \)をテイラー展開すると、
$$ (x+1)^i = \sum_{j=0}^\infty \begin{pmatrix}i\\j\end{pmatrix} x^j $$となる。\( i = -n, \, x = -(1-p) \)を代入すると
$$ p^{-n} = \sum_{j=0}^\infty \begin{pmatrix}-n\\j\end{pmatrix} \{-(1-p)\}^j = \sum_{j=0}^\infty \begin{pmatrix}j+n-1\\j\end{pmatrix} (1-p)^j $$したがって、
$$ \sum_{j=0}^\infty f(j|n,p) = \sum_{j=0}^\infty \begin{pmatrix}j+n-1\\j\end{pmatrix} p^n (1-p)^j = 1 $$
上記証明にあるように、二項係数を負の整数に拡張しているため、負の二項分布と呼ばれている。
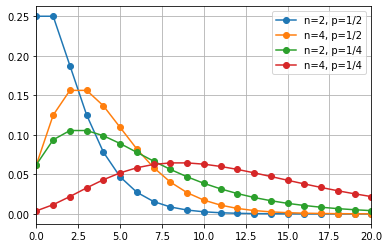
平均値
負の二項分布\( NB(n,p) \)の平均値は\( \displaystyle \frac{n(1-p)}{p} \)である。
確率変数\( X \)が\( NB(n,p) \)に従うとする。平均値\( E[X] \)を計算する。
$$ \begin{eqnarray*} E[X] &=& \sum_{i=0}^\infty if(i|n,p) \\
&=& \sum_{i=0}^\infty i \begin{pmatrix}i+n-1\\i\end{pmatrix} p^n (1-p)^i \\
&=& \sum_{i=0}^\infty i \cdot \frac{(i+n-1)!}{i!(n-1)!} p^n (1-p)^i \\
&=& \sum_{i=0}^\infty n \cdot \frac{(i+n-1)!}{(i-1)!n!} p^n(1-p)^i \\
&=& \frac{n(1-p)}{p} \sum_{i=1}^\infty \begin{pmatrix}i+n-1\\i-1\end{pmatrix} p^{n+1} (1-p)^{i-1} \\
&=& \frac{n(1-p)}{p} \sum_{i=0}^\infty \begin{pmatrix}i+n\\i\end{pmatrix} p^{n+1} (1-p)^i \\
&=& \frac{n(1-p)}{p} \sum_{i=0}^\infty \begin{pmatrix}i+n\\i\end{pmatrix} f(i|n+1,p) \\
&=& \frac{n(1-p)}{p}
\end{eqnarray*} $$
分散
負の二項分布\( NB(n,p) \)の分散は\( \displaystyle \frac{n(1-p)}{p^2} \)である。
確率変数\( X \)が\( NB(n,p) \)に従うとする。まずは\( E[X^2] \)を計算する。
$$ \begin{eqnarray*} E[X^2] &=& \sum_{i=0}^\infty i^2 f(i|n,p) \\ &=& \sum_{i=0}^\infty i(i-1)f(i|n,p) + \sum_{i=0}^\infty if(i|n,p) \\ &=& \sum_{i=2}^\infty i(i-1)f(i|n,p) + E[X] \\ &=& \sum_{i=2}^\infty i(i-1) \begin{pmatrix}i+n-1\\i\end{pmatrix} p^n(1-p)^i + E[X] \\ &=& \sum_{i=2}^\infty i(i-1) \cdot \frac{(i+n-1)!}{i!(n-1)!} p^n(1-p)^i + E[X] \\ &=& \sum_{i=2}^\infty (n+1)n \cdot \frac{(i+n-1)!}{(i-2)!(n+1)!} p^n(1-p)^i + E[X] \\ &=& \frac{(n+1)n(1-p)^2}{p^2} \sum_{i=2}^\infty \begin{pmatrix}i+n-1\\i-2\end{pmatrix} p^{n+2}(1-p)^{i-2} + E[X] \\ &=& \frac{(n+1)n(1-p)^2}{p^2} \sum_{i=0}^\infty \begin{pmatrix}i+n+1\\i\end{pmatrix} p^{n+2}(1-p)^{i} + E[X] \\ &=& \frac{(n+1)n(1-p)^2}{p^2} \sum_{i=0}^\infty f(i|n+2,p) + E[X] \\ &=& \frac{(n+1)n(1-p)^2}{p^2} + \frac{n(1-p)}{p} \end{eqnarray*} $$以上より
$$ \begin{eqnarray*} V[X] &=& E[X^2] \, – E[X]^2 \\
&=& \frac{(n+1)n(1-p)^2}{p^2} + \frac{n(1-p)}{p} \, – \frac{n^2(1-p)^2}{p^2} \\
&=& \frac{n(1-p)}{p^2}
\end{eqnarray*} $$
再生性
\( 2 \)つの確率変数\( X_i \, (i=1,2) \)がそれぞれ負の二項分布\( NB(n_i,p) \)に従うとする。
このとき、\( X_1+X_2 \)は\( NB(n_1+n_2,p) \)に従う。
確率分布\( P(X_1+X_2=x | n_1,n_2,p) \)を計算する。
$$ \begin{eqnarray*} && P(X_1+X_2=x | n_1,n_2,p) \\ &=& \sum_{i=0}^x f(i|n_1,p) f(x-i|n_2,p) \\ &=& \sum_{i=0}^x \begin{pmatrix}i+n_1-1\\i\end{pmatrix} p^{n_1} (1-p)^i \begin{pmatrix}x-i+n_2-1\\x-i\end{pmatrix} p^{n_2} (1-p)^{x-i} \\ &=& p^{n_1+n_2} (1-p)^x \sum_{i=0}^x \begin{pmatrix}i+n_1-1\\i\end{pmatrix} \begin{pmatrix}x-i+n_2-1\\x-i\end{pmatrix} \end{eqnarray*} $$ここで、二項係数について、\( \displaystyle \begin{pmatrix}i\\j\end{pmatrix} = (-1)^{-j} \begin{pmatrix}j-i-1\\j\end{pmatrix} \)が成り立つので、
$$ \begin{eqnarray*} && P(X_1+X_2=x | n_1,n_2,p) \\ &=& p^{n_1+n_2} (1-p)^x \sum_{i=0}^x (-1)^i \begin{pmatrix}-n_1\\i\end{pmatrix} (-1)^{x-i} \begin{pmatrix}-n_2\\x-i\end{pmatrix} \\ &=& p^{n_1+n_2} (1-p)^x (-1)^x \sum_{i=0}^x \begin{pmatrix}-n_1\\i\end{pmatrix} \begin{pmatrix}-n_2\\x-i\end{pmatrix} \end{eqnarray*} $$さらに、ヴァンデルモンドの畳み込みより、\( \displaystyle \begin{pmatrix}a+b\\x\end{pmatrix} = \sum_{i=0}^x \begin{pmatrix}a\\i\end{pmatrix} \begin{pmatrix}b\\x-i\end{pmatrix} \)が成り立つので、
$$ \begin{eqnarray*} P(X_1+X_2=x | n_1,n_2,p) &=& p^{n_1+n_2} (1-p)^x (-1)^x \begin{pmatrix}-(n_1+n_2)\\x\end{pmatrix} \\ &=& p^{n_1+n_2} (1-p)^x \begin{pmatrix}x+(n_1+n_2)-1\\x\end{pmatrix} \\ &=& f(x|n_1+n_2,p) \end{eqnarray*} $$ゆえに\( X_1+X_2 \)は\( NB(n_1+n_2,p) \)に従う。