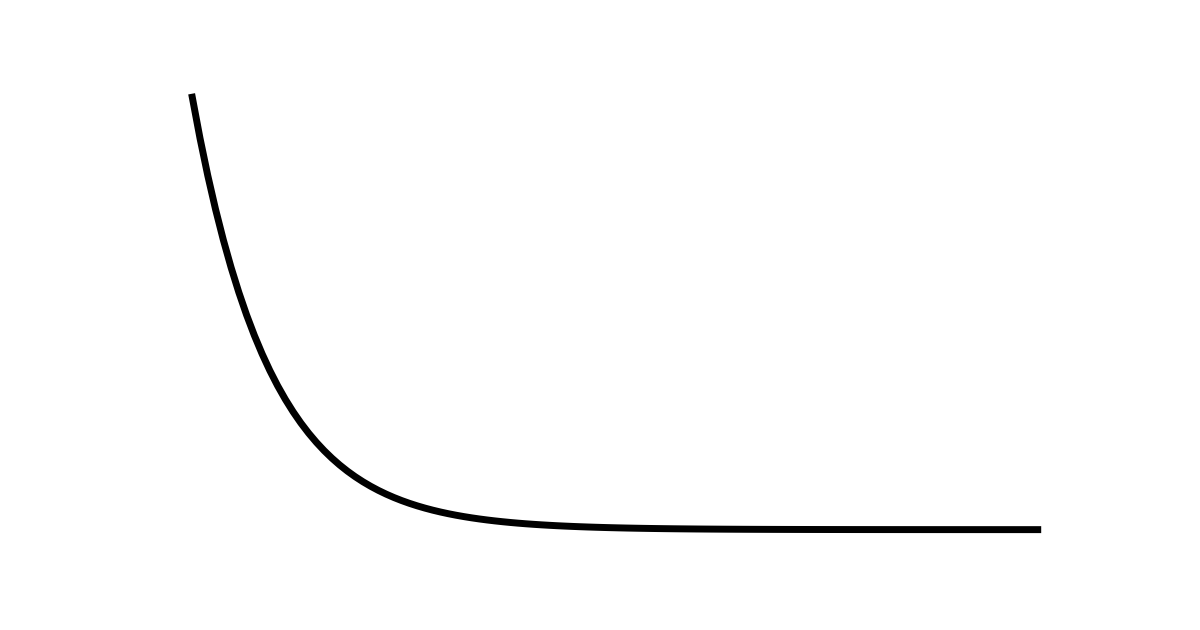
指数分布は代表的な確率分布の\( 1 \)つであり、耐用年数や災害が発生するまでの期間を求める際に利用されます。
| 定数 | \( \lambda \quad (\lambda > 0) \) |
| 確率密度関数 | \( f(x) = \left\{ \begin{array}{ll} \lambda e^{-\lambda x} & (x \geq 0)\\ 0 & (x<0) \end{array} \right. \) |
| 平均値 | \( \displaystyle \frac{1}{\lambda} \) |
| 分散 | \( \displaystyle \frac{1}{\lambda^2} \) |
定義
定数\( \lambda \quad (\lambda>0) \)を用いて、確率密度関数
$$ f(x) = \left\{ \begin{array}{ll} \lambda e^{-\lambda x} & (x \geq 0)\\ 0 & (x<0) \end{array} \right. $$で定義される確率分布を指数分布といい、\( Ex(\lambda) \)と書く。
指数分布はその定義式で指数関数を使用しているため、指数分布と呼ばれています。
耐用年数や災害が発生するまでの期間を求める際に利用されます。
すなわち、ある出来事が起こるまでの期間を求める為に利用されます。
全ての\(x \in \mathbb{R} \)に対して、\( f(x)>0 \)であることは明らかなので、積分値が\(1\)になることを示せばよい。
$$ \int_{-\infty}^\infty f(x) dx = \int_0^\infty \lambda e^{-\lambda x} dx = \left[ e^{-\lambda x} \right]_0^\infty = 1 $$したがって\( f(x) \)は密度関数である。
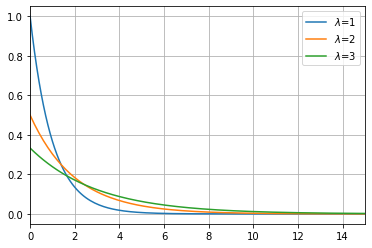
平均値
指数分布\( Ex(\lambda) \)の平均値は\( \displaystyle \frac{1}{\lambda} \)である。
確率変数\( X \)が指数分布\( Ex(\lambda) \)に従うとする。
このとき、平均値\( E[X] \)を計算する。
$$ \begin{eqnarray*} E[X] &=& \int_{-\infty}^\infty xf(x)dx \\ &=& \int_0^\infty \lambda xe^{-\lambda x}dx \\ &=& \left[ -xe^{-\lambda x} \right]_0^\infty + \int_0^\infty e^{-\lambda x}dx \\ &=& 0 + \left[ – \frac{1}{\lambda} e^{-\lambda x} \right]_0^\infty \\ &=& \frac{1}{\lambda} \end{eqnarray*} $$
分散
指数分布\( Ex(\lambda) \)の分散は\( \displaystyle \frac{1}{\lambda} \)である。
確率変数\( X \)が指数分布\( Ex(\lambda) \)に従うとする。
まず、\( E[X^2] \)を計算する。
$$ \begin{eqnarray*} E[X^2] &=& \int_{-\infty}^\infty x^2 f(x)dx \\ &=& \int_0^\infty \lambda x^2 e^{-\lambda x}dx \\ &=& \left[-x^2 e^{-\lambda x} \right]_0^\infty + \int_0^\infty 2xe^{-\lambda x}dx \\ &=& 0 + \frac{2E[X]}{\lambda} = \frac{2}{\lambda^2} \end{eqnarray*} $$したがって、分散\( V[X] \)は
$$ V[X] = E[X^2] – E[X]^2 = \frac{2}{\lambda^2} – \frac{1}{\lambda^2} = \frac{1}{\lambda^2} $$
無記憶性
無記憶性とは、前までの事象に依存しないという性質です。
例えば、「災害が発生したから次は発生しないということはない」ということです。
連続型の確率分布で無記憶性を持つものは指数分布のみとなります。
確率変数\( X \)が指数分布\( Ex(\lambda) \)に従うとする。このとき、
$$ P(X \geq a+b \, | \, X \geq a) = P(X \geq b) \qquad (a \geq 0, \, b \geq 0)$$が成り立つ。これを無記憶性を持つという。
逆に、連続分布において、無記憶性を持つ分布は指数分布のみである。
\( a \geq 0 \)に対して、
$$ P(X \geq a ) = \int_a^\infty \lambda e^{-\lambda x} dx = \left[ -e^{-\lambda x} \right]_a^\infty = e^{-\lambda a} $$条件付確率の定義より、
$$ P( X \geq a+b \, | \, X \geq a ) = \frac{P( X \geq a+b, \, X \geq a )}{P(X \geq a )} $$さらに、事象について、\( \{ X \geq a+b \, | \, X \geq a \} = \{ X \geq a+b \} \)が成り立つので、
$$ \begin{eqnarray*} P( X \geq a+b \, | \, X \geq a ) &=& \frac{P( X \geq a+b )}{P(X \geq a )} \\ &=& \frac{e^{-\lambda (a+b)}}{e^{-\lambda a}} \\ &=& e^{-\lambda b} \\ &=& P(X \geq b) \end{eqnarray*}$$したがって、無記憶性が成り立つ。
確率変数\( X \)が無記憶性を持つ連続分布に従うと仮定する。
$$ P(X \geq a+b \, | \, X \geq a) = P(X \geq b) \qquad (a \geq 0, \, b \geq 0)$$ここで、条件付確率の定義と事象について、\( \{ X \geq a+b \, | \, X \geq a \} = \{ X \geq a+b \} \)が成り立つので、
$$ P(X \geq a+b) = P(X \geq a) P(X \geq b) $$\( Q(a) = P(X \geq a) \)とおくと、\( Q(a+b)=Q(a)Q(b) \)が成り立つ。
このとき、\( n \in \mathbb{N} \)に対して
$$ \begin{eqnarray*} Q(n) &=& Q(n-1)Q(1) \\ &=& Q(n-2)Q(1)^2 \\ && \cdots \\ &=& Q(1)^n \end{eqnarray*} $$同様にして、
$$ Q(1) = Q \left( \frac{n}{n} \right) = Q \left( \frac{1}{n} \right)^n $$したがって、\( \displaystyle Q \left( \frac{1}{n} \right) = Q(1)^\frac{1}{n} \)が成り立つ。
ゆえに\( m,n \in \mathbb{N} \)に対して、\( \displaystyle Q \left( \frac{m}{n} \right) = Q(1)^\frac{m}{n}\)が成り立つので、
\( r \in \mathbb{Q}_{>0} \)に対して、\( Q(r) = Q(1)^r \)が成り立つ。
\( \alpha \in \mathbb{R}_{>0} \)に対して、有理数列\( \displaystyle \{ r_n \} \subset \mathbb{Q}_{>0}, \, \lim_{n \rightarrow \infty} r_n = \alpha \)を定義する。
ここで、\( Q(a) \)は定義から連続であるから、
$$ G( \alpha ) = \lim_{n \rightarrow \infty} G( r_n ) = \lim_{n \rightarrow \infty} G(1)^{r_n} = G(1)^\alpha $$ここで、\( \lambda = \, – \log G(1) \)とおくと、
$$ G(\alpha) = G(1)^\alpha = e^{- \alpha \log G(1)} = e^{- \lambda \alpha} $$\( \displaystyle \lim_{\alpha \rightarrow \infty} e^{- \lambda \alpha} = \lim_{\alpha \rightarrow \infty} G(\alpha) = \lim_{\alpha \rightarrow \infty} P(X \geq \alpha) = 0 \)であるから、\( \lambda > 0 \)となる。以上より、
$$ P(X \geq a) = G(a) = e^{-\lambda a} \qquad (\lambda > 0) $$ゆえに\( X \)は指数分布\( Ex(\lambda) \)に従う。